المسافة الإقليدية
المسافة الإقليدية (Euclidean distance) المسافة الإقليدية هي أقصر مسافة مستقيمة بين نقطتين في فضاء متعدد الأبعاد يرمز للأبعاد بنون (N) يُعرف أيضًا باسم الفضاء الإقليدي. يتم استخدامه كمقياس مشترك لقياس التشابه بين نقطتي بيانات ويستخدم في مجالات مختلفة مثل الهندسة وعلم البيانات (Data Science) والتعلُّم العميق (Deep Learning) وغيرها.
يُعرف أيضًا بالمعيار الإقليدي، المقياس الإقليدي، المعيار L2 ، L2 المتري والمتر الفيثاغوري.
المعادلة الإقليدية لحساب أقصر مسافة بين نقطتين هي:
مربع المسافة بين نقطتين = (س1-س2)²+ (ص1-ص2)²
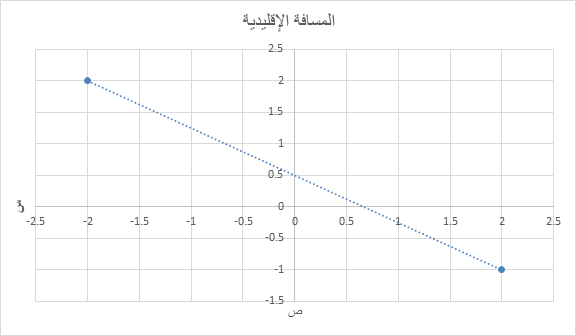
لنقوم بحساب المسافة الإقليدية بين النقطتين (2,-1) و (-2,2)
مربع المسافة بين (2,-1) و (-2,2) = (2- (-2))²+ ((-1)-2)²
مربع المسافة الإقليدية=25، المسافة=الجذر التربيعي(25)
المسافة=5
يمكن استخدام المسافة الإقليدية في فضاء ثلاثي ورباعي وعدم منتهي الأبعاد فقط بإضافة الفرق بين النقاط الجديدة في الفضاء حسب المعادلة التاليه:
مربع المسافة بين النقاط (ن) = (س1-س2)² + (ص1-ص2)² + (ن1-ن2)² + ….
مسافة منهاتن
كما تعلمنا سابقاً فإن المسافة الإقليدية هي أقصر مسافة مستقيمة بين نقطتين، ولكن المسافة الإقليدية لا تبدو عمليةً في حياتنا لحساب المسافة التي سنقطعها بين نقطتين، فغالباً يتم تصميم الشوارع ومناطق السكن بشكل مربع كما في منطقة منهاتن وسط نيويورك التي منها جائت تسمية مسافة منهاتن (Manhattan Distance). فمسافة منهاتن هي المسافة بين نقطتين تشكلان ضلعا المثلث قائم الزاوية كما في الشكل في الأسفل:
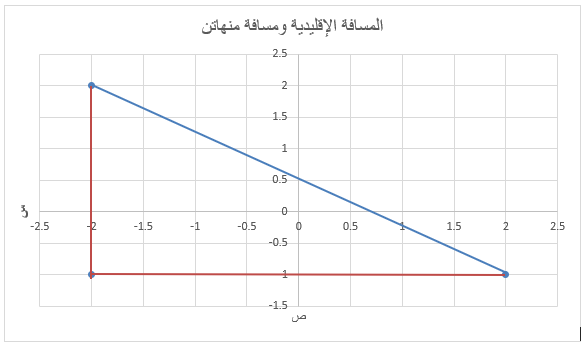
مسافة منهاتن بين نقطتين = |س1 – س2 | + |ص1 – ص2 |
مسافة منهاتن بين (2,-1) و (-2,2) = |2 – (-2) | + |-1 – 2|
المسافة = 7
وجدنا أن المسافة المقطوعة حسب منهاتن أكبر من مسافة إقليد والسبب أنه وفي حياتنا العادية لا نصل من نقطة إلى أخرى بشكل أفقي ومستقيم.
مسافة مينكوفسكي
مسافة مينكوفسكي (Minkowski Distance) هي قياس المسافة / التشابه بين نقطتين في فضاء المتجه المعياري (فضاء حقيقي ذو أبعاد ن) وهو تعميم للمسافة الإقليدية ومسافة مانهاتن.
مسافة مينكوفسكي = الجذر للقوة ن ( (س1-س2)ن + (ص1-ص2)ن + (ج1-ج2)ن + …. )
المراجع
- المسافة الإقليدية، تم استرجاع الصفحة في 02-02-2021.
- مسافة مانهاتن، تم استرجاع الصفحة في 02-02-2021.
- مسافة مينكوفسكي، تم استرجاع الصفحة في 02-02-2021.
![]()
One Reply to “المسافة الإقليدية ومسافة منهاتن”